Logarithmic Analysis: Rules, Examples, & Formulas Explained

Logarithmic analysis plays a crucial role in simplifying complex mathematical computations, transforming them into more manageable forms. As one delves deeper into the study of logarithms, it becomes evident that understanding their rules, properties, and applications is vital for mathematicians, scientists, and engineers alike. Through this comprehensive exploration of logarithmic analysis, we aim to demystify logarithmic functions and highlight their significance in various scientific disciplines.

From their historical origins to contemporary applications, logarithms have undergone extensive development, providing invaluable tools for simplifying logs and enhancing calculations. Whether it involves expressing logarithms in different bases or employing the logarithm scale in data representation, the versatility of logarithmic functions cannot be overstated. This article promises to equip readers with the foundational knowledge required to navigate the world of logarithmic calculations, encompassing essential examples, formulas, and problem-solving techniques.

What Are Logarithms?

Logarithms are mathematical expressions that indicate the power to which a base number must be raised to produce a given number. Mathematically, the logarithm of a number is defined as follows: if b is the base and y is the number, then the logarithm of y to the base b is expressed as log_b(y) = x, where b^x = y. Logarithms simplify various mathematical tasks, especially multiplication and division, by converting them into simpler functions of addition and subtraction.

For instance, using the logarithmic identity log_b(xy) = log_b(x) + log_b(y), we can condense complex multiplications into easier additions. There are several types of logarithms, with the most commonly used being the natural logarithm (base e) and the common logarithm (base 10). Understanding the definition and properties of logarithms is essential in mastering more complex mathematical concepts.

History of Logarithms: From Napier to Modern Usage

The invention of logarithms is attributed to Scottish mathematician John Napier, who introduced this concept to the mathematical community in 1614. Napier observed that by reducing multiplication into addition, complex calculations could be performed much more efficiently. His work laid the foundation for further advancements in logarithmic theory. Following Napier's groundbreaking discovery, mathematician Henry Briggs further developed the idea of logarithms by promoting the use of base 10 numbers, which led to the creation of common logarithms.

Logarithms gained immense popularity during the 17th and 18th centuries. The publication of logarithmic tables made them accessible to many fields, improving navigation, astronomy, and engineering. Many scientists, such as Galileo and Newton, utilized logarithms to simplify their work. The invention of mechanical calculating machines and, later, computers prompted a decline in the reliance on logarithmic tables; however, the underlying principles of logarithms remain foundational in today's mathematical challenges.

Understanding the Logarithmic Function

The logarithmic function can be viewed as the inverse of the exponential function. While the exponential function takes a base and exponent to yield a number, the logarithmic function begins with the number and determines the exponent that produced it. This relationship is crucial for solving equations involving exponential growth or decay, often encountered in disciplines such as biology, finance, and physics.

To express this more formally, if y = b^x, then x = log_b(y). Using this fundamental relationship, one can solve various mathematical problems by manipulating the logarithmic expressions appropriately. This process highlights the importance of familiarizing oneself with core principles of logarithmic analysis to achieve successful log solutions. Furthermore, understanding the characteristics of logarithmic functions can provide insight into data visualization, as logarithmic scales can condense wide-ranging data into more interpretable formats.

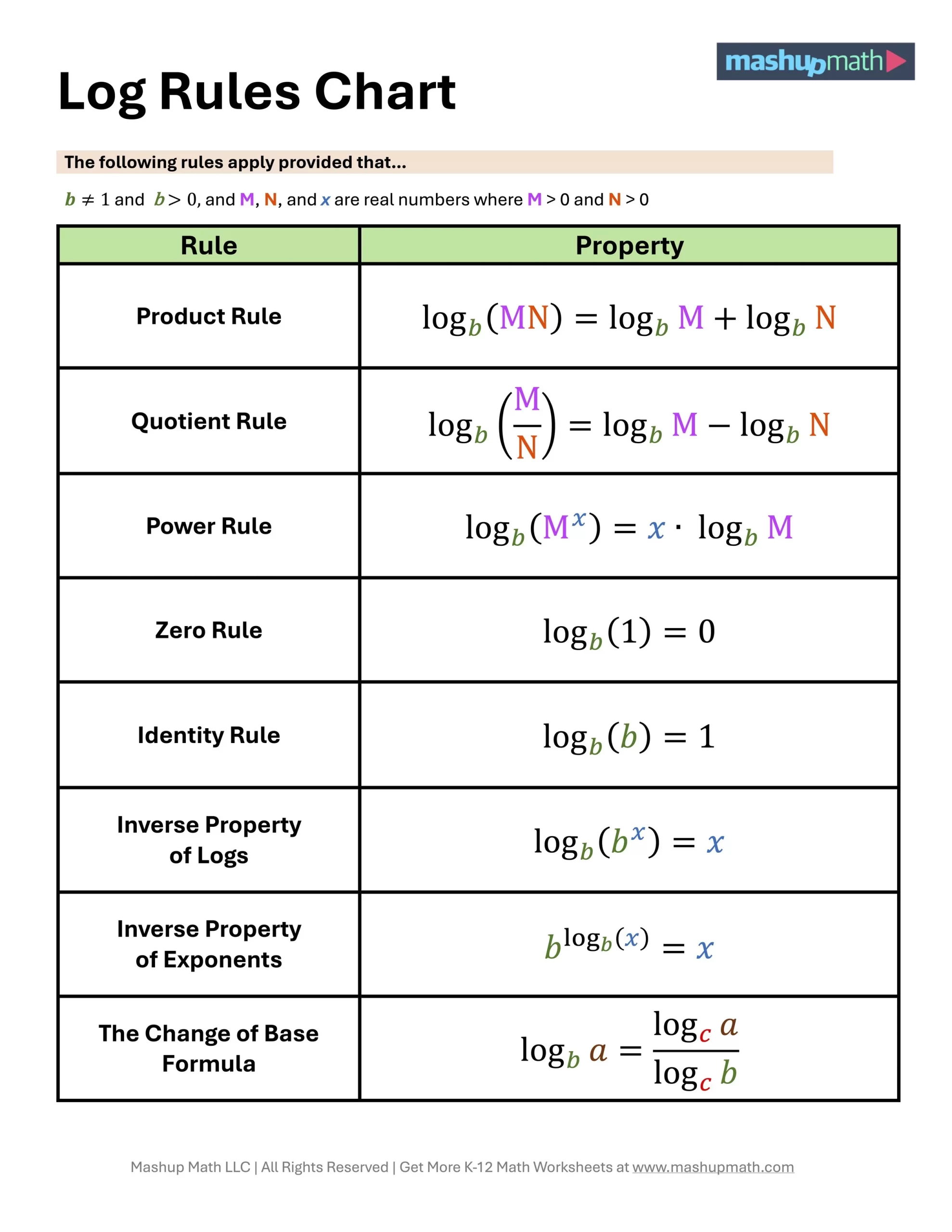
Rules of Logarithms: Key Properties Explained

The properties of logarithms, often referred to as the rules of logarithms, streamline calculations and conversions in logarithmic analysis. Here are some of the key properties to memorize:

• Product Rule: log_b(xy) = log_b(x) + log_b(y)
• Quotient Rule: log_b(x/y) = log_b(x) - log_b(y)
• Power Rule: log_b(xⁿ) = n * log_b(x)
• Change of Base Formula: log_b(x) = log_k(x) / log_k(b), for any positive number k

These rules are instrumental in s simplifying logs in various equations. For example, by utilizing the product rule, one can break down log calculations into simpler components, facilitating easier computation and understanding.

Common Logarithms vs. Natural Logarithms

Logarithms can be categorized into various types, but the most frequently used are the common logarithms and natural logarithms. Common logarithms utilize base 10 and are denoted as log(x), while natural logarithms utilize base e (approximately equal to 2.718) and are denoted as ln(x). Each type has distinct applications and benefits.

Common logarithms are generally used in scientific disciplines where measurements span several orders of magnitude, making them an essential tool in fields like chemistry and physics. On the other hand, the natural logarithm is frequently applied in calculus and mathematical modeling due to its connections with growth patterns, decay processes, and continuous compounding.

Examples of Logarithmic Calculations

To grasp logarithmic analysis deeper, let's explore some examples that illustrate how to perform calculations using logarithms:

Example 1: Basic Logarithmic Calculation

Calculate log₁₀(1000).

Using the knowledge of logarithmic properties, we find:

log₁₀(1000) = log₁₀(10³) = 3.

Example 2: Using the Product Rule

Calculate log₁₀(50).

Suppose we wish to break this down using the product rule:

log₁₀(50) = log₁₀(2 * 25) = log₁₀(2) + log₁₀(25).

Using a calculator, we will find the approximations for log₁₀(2) and log₁₀(25) to sum them up for the final result.

Applications of Logarithms in Science and Technology

Logarithms find versatile applications across various fields of science and technology. In chemistry, the pH scale utilizes logarithms to denote acidity: higher concentrations of hydrogen ions correspond to lower pH values, which can be expressed logarithmically. In biology, growth rates and decay processes frequently use natural logarithms for analysis, such as in population growth models and radioactive decay.

In technology, logarithmic scales play a pivotal role in data representation and signal processing. For instance, the decibel scale in acoustics, representing sound intensity, is a logarithmic scale that quantifies loudness in a compact format. Logarithmic analysis is also essential in computer science, particularly in algorithms and complexity theory, where logarithmic time complexity indicates efficient computations.

Logarithmic Formulas: A Comprehensive Overview

In logarithmic analysis, several key formulas are essential to understand for a complete grasp of the subject:

• log_b(x) = y implies b^y = x
• log_b(b) = 1
• log_b(1) = 0
• log_e(e) = 1
• ln(e^x) = x for any real number x

These formulas serve as foundational elements in logarithmic calculations, ensuring that practitioners can derive log solutions effectively. Moreover, familiarizing oneself with these formulas can enhance skills in solving logarithmic equations and expressing complex logarithmic terms.

How to Solve Logarithmic Equations

Solving logarithmic equations often requires a blend of fundamental logarithmic properties and algebraic methods. To demonstrate this, let’s tackle a sample problem:

Sample Equation: Solve for x

log₂(x) + log₂(4) = 5.

Applying the product rule, we can consolidate the logarithms:

log₂(4x) = 5.

Now, we can convert this logarithmic expression into its exponential form:

4x = 2⁵.

Solving for x gives us:

x = (2⁵/4) = 4.

As illustrated, using logarithmic properties can significantly facilitate the solving process, yielding efficient log solutions.

Conclusion: The Importance of Logarithmic Analysis

In conclusion, logarithmic analysis is an indispensable tool for simplifying mathematical processes, allowing for efficient calculations across various scientific and technological realms. Mastering the rules, properties, and applications of logarithms provides foundational skills necessary for future exploration in advanced mathematics, physics, engineering, and data analysis.

As we have seen, the efficacy of logarithms in expressing and solving complex problems makes them crucial to modern analytical practices. By integrating logarithmic principles into mathematical reasoning and computational methods, we can unlock deeper insights into the patterns that govern the world around us. Thus, embracing logarithmic analysis can lead to profound advancements across various disciplines, illustrating the timeless relevance of this mathematical concept.

Did you find this article helpful? Logarithmic Analysis: Rules, Examples, & Formulas Explained See more here Education.