What Are Semi-Ideal Solutions in Chemistry Explained Simply

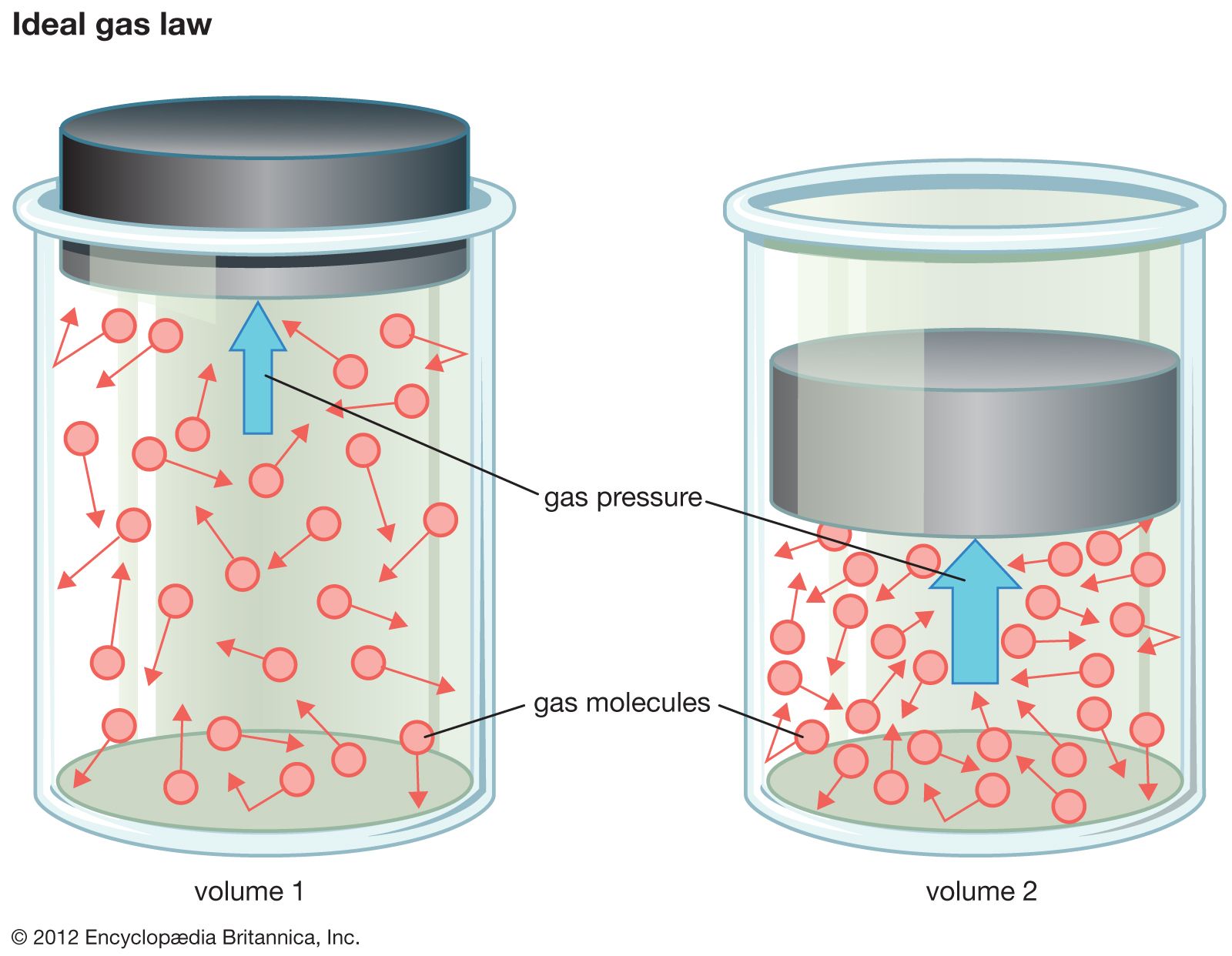
In the vast field of chemistry, understanding various types of solutions is essential to grasp the underlying principles that govern chemical interactions. One intriguing category is semi-ideal solutions, which occupy a middle ground between ideal solutions and non-ideal solutions. As we delve into this topic, we will uncover the unique characteristics that define semi-ideal solutions and why they are significant in the study of chemistry.

The concept of ideal solutions serves as a basis for comparison, where solutions exhibit linear behavior concerning their properties. However, in real-world scenarios, many solutions do not fully adhere to the ideal model. This is where semi-ideal solutions come into play, allowing chemists to better understand and predict behavior in more complex mixtures. In this article, we will explore the various facets of semi-ideal solutions—examining their types, properties, and practical implications.

Understanding Semi-Ideal Solutions

Semi-ideal solutions are defined by certain deviations from ideality, which can be attributed to how they behave upon mixing. Unlike ideal solutions, where components mix perfectly without any interaction, semi-ideal solutions exhibit some degree of interaction between the components. Such interactions can influence the overall behavior, stability, and properties of the solution.

These solutions display unique thermodynamic properties, often characterized by excess terms related to entropy and heat of mixing. Understanding these properties is crucial for chemists as they navigate the challenges posed by real chemical systems. The classification of semi-ideal solutions helps in evaluating the extent of deviation from ideal behavior and in making more accurate predictions about the solution's characteristics.

Types of Semi-Ideal Solutions

There are two principal types of semi-ideal solutions: regular solutions and athermal solutions. Each type has distinct characteristics that influence their behavior upon mixing and make it essential to differentiate between them.

Regular Solutions Explained

In regular solutions, the excess entropy (SE) is zero, indicating that there is no change in orderliness upon mixing. However, the heat of mixing (HE) is non-zero, which means that there is either an endothermic or exothermic reaction occurring as solutes dissolve. This signifies that the interactions between the solutes and solvents are unequal, leading to variations in energy. Regular solutions help illustrate the effects of solute-solvent interactions on thermodynamic behavior.

• Behavior: Regular solutions show deviations in heat of mixing while maintaining similar entropy levels.
• Applications: Useful in understanding mixtures of similar molecular structures, such as certain polymer blends.

Athermal Solutions Explained

Athermal solutions, in contrast, display zero heat of mixing (HE) but have non-zero excess entropy (SE). This indicates that while there is no energy change during mixing, the arrangement of molecules becomes disordered, leading to an increase in entropy. Athermal solutions can occur in systems where the components have similar molecular sizes and shapes, reducing the energetic effects of mixing.

• Behavior: Athermal solutions maintain the energy content but increase disorder.
• Applications: Significant for understanding systems like certain types of ideal gas mixtures where intermolecular forces are minimal.

Comparing Semi-Ideal Solutions with Ideal Solutions

When comparing semi-ideal solutions to ideal solutions, it’s essential to understand the fundamental differences. In an ideal solution, the components mix without any changes in energy or entropy, behaving according to Raoult's Law perfectly. Semi-ideal solutions, however, showcase deviations that manifest as either heat of mixing or excess entropy—indicating the complexity of real chemical systems.

These deviations imply that predictions based on ideal conditions may not accurately reflect the behavior of semi-ideal solutions. Chemists need to account for these differences to ensure their models and predictions accurately describe the systems they are studying. By understanding where semi-ideal solutions fit within the broader spectrum of solution types, researchers can develop more comprehensive theories and applications.

Importance of Semi-Ideal Solutions in Chemistry

The study of semi-ideal solutions is critical in several fields of chemistry, including physical chemistry, materials science, and chemical engineering. Recognizing the thermodynamic properties of these solutions aids in improving the efficiency of chemical processes, optimizing product formulation, and predicting solution behavior in various contexts.

• Research and Development: Understanding these solutions can lead to better solvent selection and material properties in industrial applications.
• Predictive Modeling: Enhancements in predicting phase diagrams and solubility can be achieved by factoring in deviations related to semi-ideal solutions.

Examples of Semi-Ideal Solutions

Numerous real-world examples illustrate the concept of semi-ideal solutions. One classic example is the mixture of ethanol and water, a well-studied combination that deviates from ideality due to significant hydrogen bonding. This interaction results in changes in both heat of mixing and entropy, demonstrating characteristics of a regular solution.

Another example involves polymer solutions, where mixtures of polymers with solvents often display athermal behavior. In these cases, the interactions between the polymer chains and the solvent molecules create a disordered system that leads to increased entropy despite a lack of heat change during mixing. Understanding such examples further reinforces the practical significance of semi-ideal solutions in real-world applications.

Conclusion

In conclusion, semi-ideal solutions serve as a crucial concept in understanding the behavior of mixtures that do not fully conform to ideal conditions. By exploring the types of semi-ideal solutions—including regular and athermal solutions—we gain insight into how molecular interactions affect thermodynamic properties. Recognizing these differences allows chemists to make more accurate predictions and enhance their understanding of complex chemical systems.