
AND Gate Logic: Exploring Three Basic Functions Explained
In the realm of digital electronics, AND gate logic plays a crucial role in the design and functionality of circuits. Logic gates, which form the foundation of digital systems, are used to perform basic logical functions on one or more binary inputs to produce a single binary output. Among these logic gates, the AND gate is fundamental in understanding how complex logical expressions can be constructed. By exploring three basic functions—AND, OR, and NOT—this article aims to provide a comprehensive overview of how these gates operate and their significance in digital logic.
By delving into the various logic functions, readers will gain insight not only into the mechanics of AND gate logic but also into the entire framework of logic gates that govern modern electronic devices. This exploration includes examining truth tables to understand the behavior of these functions clearly and showcasing real-world applications to emphasize their practical importance. Understanding these principles will pave the way for further exploration in the vast world of computing and electronic communications.
Understanding Logic Gates
Logic gates are the building blocks of digital circuits, enabling the performance of various logical operations on binary inputs. Each type of logic gate has a specific function that defines its behavior. The three primary logic functions are NOT, AND, and OR, each offering unique advantages when processing information in binary form. By understanding how each gate operates, we can better appreciate their role in complex logic systems.
The AND gate is a fundamental component of digital electronics, functioning through a simple principle—it outputs a true (1) result only if all its inputs are true (1). This behavior distinctly separates the AND function from the OR function, which will be discussed later. Grasping the functionality of these gates allows for the development of more intricate circuits that can perform various computational tasks.
The NOT Function: Inversion Explained
The NOT function, also known as an inverter, is one of the simplest and most essential logic functions. This gate takes a single input and inverts it, providing an output that is the opposite of the input. For example, if the input is true (1), the output will be false (0), and vice versa. This basic operation is crucial for creating more complex logic expressions, enabling engineers and designers to manipulate digital signals effectively.
Through the application of the NOT function, circuits can perform negation operations, which is vital in creating decision structures in programming and numerous electronic devices. The use of NOT gates can simplify the implementation of other logic functions and is often seen in various digital systems. Understanding how the NOT function works is a foundational step toward grasping the intricacies of more complex gates.
The AND Function: Conditions for True Output
The AND function operates on multiple inputs to determine whether all conditions are met for the output to be true (1). Specifically, an AND gate will only yield an output of true (1) when every one of its inputs is also true (1). If at least one input is false (0), the output will be false (0). This characteristic makes the AND function particularly useful in various logical operations and real-world applications, including safety systems, decision-making circuits, and binary operations.
For example, when implementing a security system that requires multiple criteria to be satisfied before granting access, the AND gate becomes vital. Only when each required criterion (such as a valid password and fingerprint recognition) is true will the system activate an output, such as opening a door. Thus, the AND gate logic not only influences the design of electronic circuits but also impacts the efficiency and reliability of systems in everyday use.
The OR Function: At Least One True Input
The OR function differs from the AND function in its operation, producing a true output (1) as long as at least one of its inputs is true (1). This means that the output will only be false (0) when all inputs are false (0). The OR function is essential in scenarios where the occurrence of one condition is sufficient for a desired output, such as notifications in alarms or alerts.
For instance, in a simple alert system that activates an alarm if either a motion sensor detects movement or a door sensor is triggered, an OR gate would be utilized. In this case, the system generates a true signal (1) if any of the sensors signal true (1), thereby ensuring safety. Thus, understanding the OR function is key to designing efficient and responsive electronic systems.
Truth Tables: Visualizing Logic Functions
One of the most effective ways to understand and visualize the behavior of AND gate logic, as well as other logic functions, is through the use of truth tables. A truth table systematically lays out all possible input combinations and provides the corresponding output for each combination. This method aids in comprehending how each logic gate behaves under various circumstances.
Here’s how truth tables look for the basic functions:
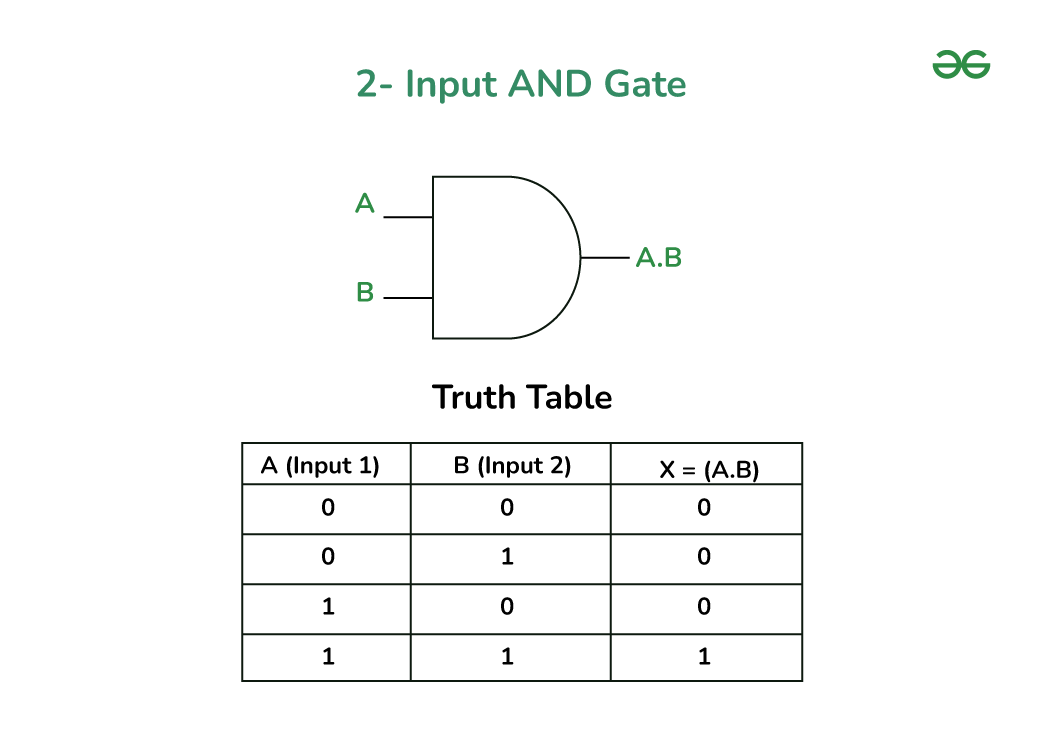
Truth Table for AND Gate
| Input A | Input B | Output (A AND B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
As shown in the table, the output of an AND gate is only true (1) when both inputs are true (1). The other combinations yield a false (0) output. This representation is indispensable for designing circuits and understanding logic interactions clearly.
Truth Table for OR Gate
| Input A | Input B | Output (A OR B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Similarly, the OR gate table shows that the output is true (1) when at least one input is true. This clear representation of logic behaviors not only aids in understanding digital logic functions but also assists in developing logical circuits accurately.
Applications of AND Gates in Real-World Circuits
The real-world applications of AND gate logic span a variety of fields, including telecommunications, computing, and safety systems. Their ability to ensure that multiple conditions are met before providing an output makes them pivotal in safety mechanisms, automated systems, and data processing units. In telecommunications, AND gates are often employed in protocols that require multiple confirmations before proceeding with data transmissions.
Safety systems, too, leverage the reliance on AND gates for functions where the joint activation or status signals determine outcomes. For example, in automotive systems, an AND gate may link inputs from seatbelt sensors and ignition systems to prevent the car from starting without the driver securely buckled. This use of AND gate logic exemplifies how logical functions manage critical operations and enhance user safety.
Conclusion: The Importance of Logic Functions in Computing
The study of logic gates, specifically AND gate logic, highlights their essential roles in modern computing and electronics. Understanding the core functions of AND, OR, and NOT gates provides invaluable insights into how electronic systems operate. The ability to analyze and design digital circuits is key to advancements in technology and plays a vital role in developing more sophisticated electronic devices.
As our reliance on digital devices continues to grow, the understanding of these fundamental logic functions becomes even more crucial. Logic gates not only form the backbone of computing technology but also drive innovations in various applications, from security systems to complex algorithms. It is evident that mastering these concepts and their practical applications is fundamental in today’s digital-driven world.
Further Reading: Expanding Your Knowledge of Logic Gates
To broaden your understanding of AND gate logic and its applications, consider exploring additional resources that delve deeper into digital electronics, circuit design, and logical expressions. Textbooks, online courses, and tutorials dedicated to digital logic design can offer more comprehensive knowledge and practical insights.
Expanding your knowledge in this area will not only strengthen your comprehension of logic gates but also enhance your skills in computer science, engineering, and various technologies. Continuous learning in the field of digital electronics will empower you to tackle more advanced concepts and contribute effectively to future technological developments.
Did you find this article helpful? AND Gate Logic: Exploring Three Basic Functions Explained See more here Education.
Leave a Reply





Related posts